गणितको रहस्यमय संसारमा एक चमत्कार!

२०८२ श्रावण १६ गते

गणितलाई प्रायः कठिन र शुष्क विषयको रूपमा लिइन्छ। तर वास्तवमा गणित एउटा यस्तो रहस्यमय क्षेत्र हो, जहाँ साना-साना संख्याहरूले ठूलो आश्चर्य ल्याउन सक्छन्। यस्ता संख्याहरूले केवल विद्यार्थी मात्र होइन, विश्वभरका गणितज्ञहरूलाई समेत अचम्ममा पार्ने गर्छन्। त्यस्ता नै केही अद्भुत संख्याहरू प्रस्तुत गरिएको छ।

अद्भुत संख्या २५२०, गणितको चमत्कार!

गणितमा केही संख्याहरू यस्ता हुन्छन्, जसले हामीलाई सोच्न बाध्य पार्छन्। यस्तो नै एउटा संख्या हो, २५२०।
सामान्य देखिने यो अंकले विश्वभरका गणितज्ञहरूलाई चकित तुल्याएको छ। भारतका महान गणितज्ञ श्री श्रीनिवास रामानुजनले आफ्नो अद्वितीय बुद्धिमत्ता र गहिरो अध्ययनबाट यस अद्भुत तथ्यलाई उजागर गरेका थिए।

उनले देखाए, गणित केवल संख्या होइन, समय, संस्कार र ब्रह्माण्डसँगको सम्बन्ध पनि हो।

के हो २५२० को रहस्य?

२५२० यस्तो पहिलो सानो संख्या हो, जसले १ देखि १० सम्मका सबै पूर्ण संख्यालाई बिना कुनै बाँकी भाग लिन्छ।

उदाहरणका लागि:

२५२० ÷ १ = २५२०  
२५२० ÷ २ = १२६०  
२५२० ÷ ३ = ८४०  
२५२० ÷ ४ = ६३०  
२५२० ÷ ५ = ५०४  
२५२० ÷ ६ = ४२०  
२५२० ÷ ७ = ३६०  
२५२० ÷ ८ = ३१५  
२५२० ÷ ९ = २८०  
२५२० ÷ १० = २५२

यो देखेर जो कोही अचम्मित हुन्छ। सामान्यतया, यस्तो संख्याको अस्तित्व असम्भव जस्तै लाग्छ, तर गणितले सम्भव बनाएको छ!

कसरी बन्यो यो संख्या?

२५२० लाई यसरी पनि बुझ्न सकिन्छ:

२५२० = ७ × ३० × १२

अनि यी संख्याहरू खाली अंक मात्र होइनन्, यी हाम्रो जीवनसँग जोडिएका छन्:

हप्ता — ७ दिन
महिना — ३० दिन (औसत)
वर्षमा — १२ महिना

यी तीनलाई गुणा गर्दा: ७ × ३० × १२ = २५२०

२५२० मात्र होइन, गणितमा यस्ता धेरै संख्याहरू छन्, जसले अचम्म पार्ने अद्भुत गुणहरू बोकेका हुन्छन्। यहाँ केही रोचक र चमत्कारिक संख्याहरू प्रस्तुत गरिएका छन्।

१७२९ रामानुजन संख्या

यो संख्या श्रीनिवास रामानुजन र घोडे हार्डीको कथाबाट प्रसिद्ध छ।

१७२९ यस्तो सानो संख्या हो, जुन दुई फरक तरिकाले दुई घन संख्याहरूको योगबाट आउँछ:

1729 = 1³ + 12³ = 9³ + 10³

४०७ आर्मस्ट्रङ्ग संख्या (Armstrong Number)

४०७ = 4³ + 0³ + 7³
= 64 + 0 + 343 = 407

यो यस्तो संख्या हो जसको प्रत्येक अंकको घनफल जम्मा गर्दा त्यही संख्या नै आउँछ।

यस्ता संख्या १ देखि १००० भित्र थोरै मात्र छन्:

153, 370, 371, 407

८९ Fibonacci जादू संख्या

यदि तपाईं Fibonacci Series (0, 1, 1, 2, 3, 5, 8, 13,…) जान्नुहुन्छ भने,
८९ एक यस्तो संख्या हो जसलाई Fibonacci संख्याहरूले गुणा गरेर प्राप्त हुन्छन्।

Fibonacci series को प्रत्येक अंकलाई क्रमशः घट्दो क्रममा गुणा गरेर जम्मा गर्दा ८९ नै आउँछ:
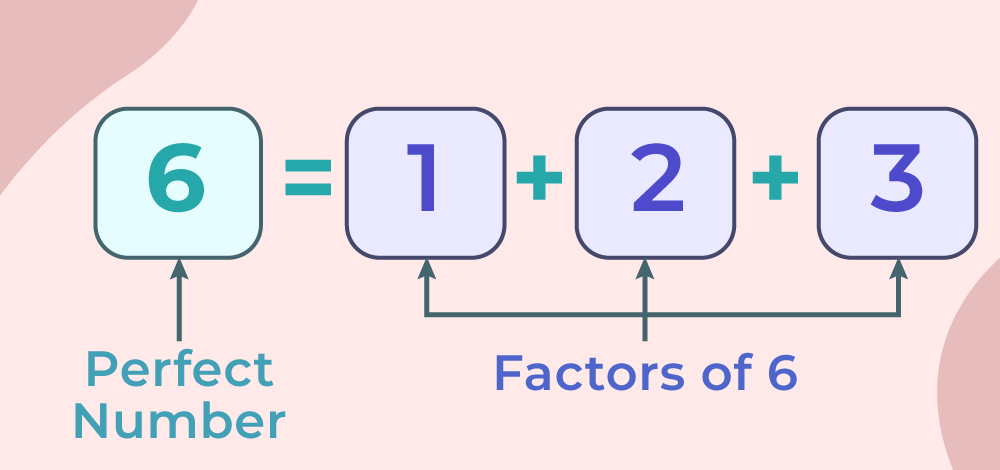
0×1 + 1×1 + 1×2 + 2×3 + 3×5 + 5×8 + … = ८९

६ सबैभन्दा सानो परिपूर्ण संख्या (Perfect Number)

6 को गुणनफल गर्ने सबै साना संख्याहरू: 1, 2, 3
तीलाई जोड्दा: 1 + 2 + 3 = 6

त्यस्ता अरू संख्याहरू: 28, 496, 8128 आदि

यी संख्याहरूले हामीलाई सिकाउँछन् कि गणित केवल सूत्र वा अंकहरूको खेल होइन, यो एउटा ज्ञान, समय र सौन्दर्यको संयोजन हो।
यस्ता चमत्कारी तथ्यहरूबाट प्रेरणा लिएर गणितसँग मित्रता गर्न थाले, भने गणित वास्तवमै रमाइलो र जीवनोपयोगी विषय बन्न सक्छ।

यो समाचार तपाईलाई कस्तो लाग्यो??